KVA
KVA stands for “kilovolt-ampere,” and it is a unit of electrical power used to measure apparent power in an electrical circuit. Apparent power is the combination of real power (in kilowatts, kW) and reactive power (in kilovars, kVAR). KVA does not represent actual power consumption but rather the total power in an electrical system, taking into account both the active and reactive components.
In simple terms, KVA represents the total electrical power that is flowing through a circuit, including any power that may be lost due to factors like inductive or capacitive reactance. It is an important metric in electrical engineering and is used for sizing transformers, generators, and other electrical equipment to ensure they can handle the total power demands of a system.
The formula to calculate KVA is:
KVA = (Voltage (V) × Current (I)) / 1000
Where:-
- Voltage (V) is the RMS (root mean square) voltage in volts (V).
- Current (I) is the RMS current in amperes (A).
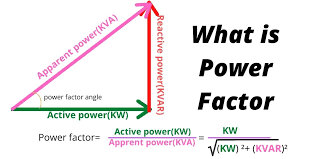
It’s important to note that KVA is a scalar quantity, and it does not take into consideration the phase difference between voltage and current, which is crucial when dealing with AC (alternating current) circuits. The concept of power factor (PF) is used to account for this phase difference and determine the actual useful power (kW) in a system. The relationship between KVA, KW, and power factor is as follows:
KW = KVA × Power Factor
In summary, KVA is a measure of apparent power in an electrical circuit, representing the total power flow, while KW represents the real or active power that is doing useful work in the circuit.
KW:-
KW stands for “kilowatt,” and it is a unit of electrical power commonly used to measure real or active power in an electrical circuit. Kilowatts represent the actual power consumed or utilized by electrical devices to perform useful work. Unlike KVA (kilovolt-ampere), which accounts for both active and reactive power, KW only considers the active power component of an electrical system.
In simple terms, KW represents the rate at which energy is being used or produced in a system. It is a crucial metric for understanding the actual power consumption of devices and equipment. The term “kilo” in kilowatt denotes a factor of 1,000, so 1 kilowatt is equivalent to 1,000 watts (W).
The formula to calculate KW is straightforward:
KW = Voltage (V) × Current (I) × Power Factor
Where:
- Voltage (V) is the RMS (root mean square) voltage in volts (V).
- Current (I) is the RMS current in amperes (A).
- Power Factor (PF) represents the efficiency or phase relationship between voltage and current. It is a dimensionless number between 0 and 1, where 1 indicates a purely resistive load with perfect alignment between voltage and current.
KW is a practical measure of how much electrical energy is being used to perform work, such as driving motors, heating elements, or lighting. It is commonly used for billing purposes by utility companies and for specifying the power ratings of electrical appliances, industrial machinery, and other devices.
In summary, kilowatts (KW) are a unit of real power that represents the actual energy consumption or utilization in an electrical system, excluding the reactive power component.
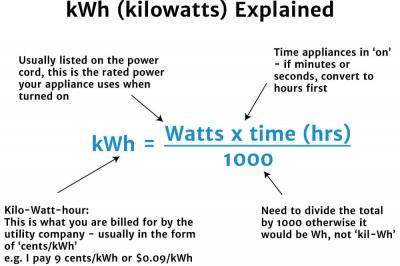
A kilowatt is simply a measure of how much power an electric appliance consumes—it’s 1,000 watts to be exact. You can quickly convert watts (W) to kilowatts (kW) by diving your wattage by 1,000: 1,000W 1,000 = 1 kW.
- Lower watts: If you are using a 100-watt device, such as a plasma TV, you would have to watch your favorite shows for 10 hours before reaching 1 kWh.
- Higher watts: If you are running a 2,000-watt appliance, such as a clothes dryer, you only need to power it for 30 minutes to reach 1 kWh.
The power you use on a daily basis can quickly add up to 1 kWh if you are frequently using high-wattage appliances in your home. Keep this in mind, as energy companies typically charge for power on a per-kWh basis.
KVAR
KVAR stands for “kilovolt-ampere reactive” and is a unit of electrical power used to measure reactive power in an electrical circuit. Reactive power is the portion of apparent power (measured in KVA) that does not perform useful work in an electrical system but instead is associated with the magnetic or capacitive properties of the components within the system. KVAR is often used in the context of AC (alternating current) electrical circuits.
In an AC circuit, there can be a phase difference (a time delay) between the voltage and current waveforms. This phase difference occurs due to inductive and capacitive elements in the circuit. Reactive power is needed to establish and maintain this phase relationship but doesn’t contribute to actual work or power delivered to a load. Instead, it’s required for tasks like magnetizing transformers or compensating for the capacitive effects of long transmission lines.
Reactive power is important because it affects the efficiency and stability of electrical systems. Excessive reactive power can lead to voltage drops, increased line losses, and decreased system capacity. Utilities and industrial facilities often manage reactive power to maintain a good power factor (the ratio of real power to apparent power) and ensure efficient power distribution.
The formula to calculate KVAR is:
KVAR = (Voltage (V) × Current (I) × sin(θ)) / 1000
Where:
- Voltage (V) is the RMS (root mean square) voltage in volts (V).
- Current (I) is the RMS current in amperes (A).
- θ (theta) represents the phase angle between voltage and current waveforms.
KVAR is a scalar quantity, and its unit, “kilovolt-ampere reactive,” is a measure of reactive power. It is typically expressed in units such as kVAR or MVAR (megavolt-ampere reactive) for larger systems. Managing reactive power is essential for maintaining a stable and efficient electrical grid and for preventing issues like voltage sag and system overloads.
