Drawings Related to Circle
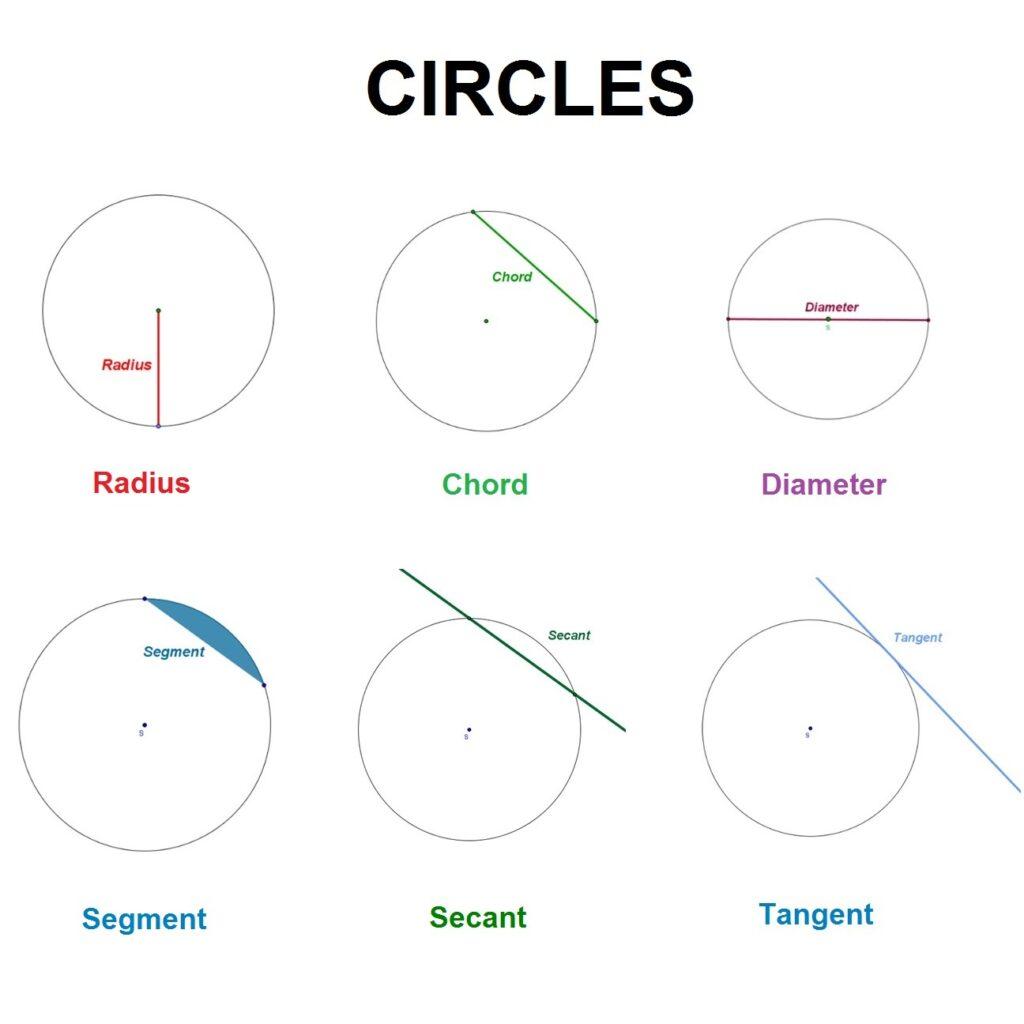
Circle:- A round plane figure whose boundary (the circumference) consists of points equidistant from a fixed point (the Centre). In geometry, a circle is a perfectly round shape, any point around its curve is the same distance from its central point. A circle consists of a closed curved line around a central point. Every point on the line is the same distance from the central point. This distance to the center is called the radius.
Parts of a Circle
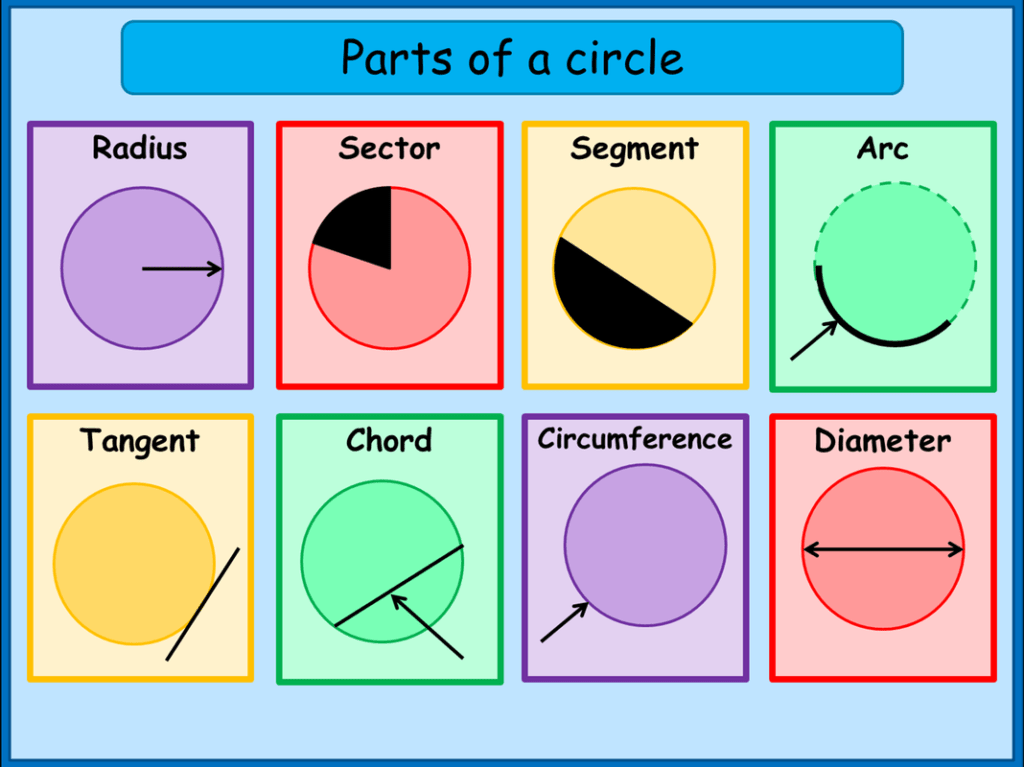
The center of a circle is the point equidistant from the points on the edge.
The diameter is the length of the line through the center that touches two points on the edge of the circle. The diameter is the length of the line through the center that touches two points on the edge of the circle.
The circumference of a circle is the perimeter of the circle. It is the total length of the boundary of the circle.
A line that touches the circle at a single point is known as a tangent to a circle
In the case of a circle, a secant intersects the circle at exactly two points. A chord is the line segment determined by the two points, that is, the interval on the secant whose ends are the two points.
A chord is a line passing from one point to another on the circumference of a circle. Diameter is also a chord that passes through the Centre.
The arc of a circle is defined as the part or segment of the circumference of a circle. A straight line that could be drawn by connecting the two ends of the arc is known as a chord of a circle. If the length of an arc is exactly half of the circle, it is known as a semicircular arc.
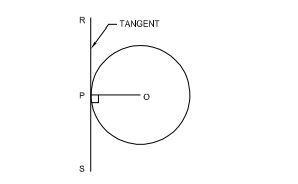
Draw a tangent to a given circle of φ 70 mm at any
point `P’ on it.
• Draw a circle of φ 50 with `O’ as centre.
• Mark the given point `P’ on the circumference of the circle.
• Join OP.
• Draw a line RS perpendicular to PO through `P’.
• RS is the tangent at `P’.
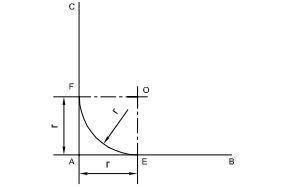
Draw an arc of given radius (R 20 mm) to touch to
two straight lines (50 mm each) at right angles.
• Draw the lines AB and AC (50 mm each) at right angles.
• With `A’ as centre and given radius (R 20 mm) draw an arc to cut lines AB and AC at E and F.
• With E and F as centres and the radius given (R 20 mm), draw arcs to intersect each other at `O’.
• Use `O’ as centre and with same radius (R 20) draw a curve (arc) which will just touch the given lines AB and A